后分布式时代: 多数派读写的’少数派’实现

本文链接: https://blog.openacid.com/algo/quorum/

前言

paxos可以看做是2次 多数派读写 完成一次强一致读写. 多数派要求半数以上的参与者(paxos中的Acceptor)接受某笔操作. 但 多数派读写 并不一定需要多于半数的参与者, 分布式系统中某些场合的优化, 可以通过减少参与者数量来完成的.

多数派读写:分布式系统的基础

分布式系统中, 其中一个基础的问题是如何在不可靠硬件(低可用性)基础上构建可靠(高可用性)的服务, 要达成这个目标, 核心的手段就是复制(例如一份数据存3个副本). 而复制过程中的一致性问题, 最后都归结为paxos的解决方案. 这些我们在 paxos的直观解释 中做了详细的介绍.

在 paxos的直观解释 的 slide-20 中, 我们了解到, paxos是通过2次 多数派读写 来完成强一致的读写:

这个方法之所以能工作也是因为多数派写中, 一个系统最多只能允许一个多数派写成功. paxos也是通过2次多数派读写来实现的强一致.

也就是说, 多数派读写 在分布式领域是一个更基础的问题. 在 paxos的直观解释 中也简单介绍了一下 多数派读写:

slide-10 为了解决半同步复制中数据不一致的问题, 可以将这个复制策略再做一改进: 多数派读写: 每条数据必须写入到半数以上的机器上. 每次读取数据都必须检查半数以上的机器上是否有这条数据.

在这种策略下, 数据可靠性足够, 宕机容忍足够, 任一机器故障也能读到全部数据.

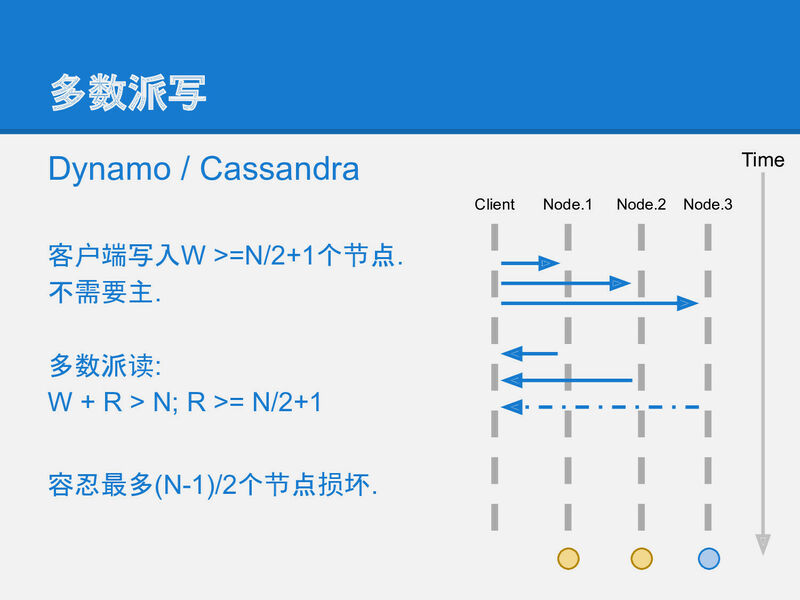
多数派读写, 也可称作 quorum-rw, wikipedia上的描述如下:

在有冗余数据的分布式存储系统当中，冗余数据对象会在不同的机器之间存放多份拷贝。但是同一时刻一个数据对象的多份拷贝只能用于读或者用于写。

算法来源于Gifford, 1979。 分布式系统中的每一份数据拷贝对象都被赋予一票。每一个读操作获得的票数必须大于最小读票数（read quorum）（Vr），每个写操作获得的票数必须大于最小写票数（write quorum）(Vw）才能读或者写。如果系统有V票（意味着一个数据对象有V份冗余拷贝），那么最小读写票数(quorum)应满足如下限制：

1. Vr + Vw > V
2. Vw > V/2

🌰 举个例子, 如果有5个存储节点{a, b, c, d, e}, 一笔操作给x赋值为3(x=3) 成功写入了abc 3个节点, 那么另外一个读, 只要联系到任意3个节点, 就一定能读到x=3 这就是安全的.

要联系到至少3个节点, 在某些场景下仍然是昂贵的, 例如一个全球分布的DB, 2个机房之间延迟可能达到上百毫秒. 我们有时希望通过减少必须参与的节点数量, 从而提升系统的性能. 于是我们先从概念开始, 看看quorum-rw中的quorum是什么:

Quorum vs Majority

在很多paper中, 是不区分quorum和majority的差别的:

• majority就是”多数派”的意思(也就是多于半数, ≥⌊n/2⌋+1), 例如5节点中选3个;

• quorum, 翻译为”法定人数”( 🤔 WT…? ), 它不一定是多数, 但需要满足一个条件, 就是任意2个quorum必须有交集(majority已经满足了这个要求). 所以在本文中, 我们将quorum看做majority概念的一个推广; majority是quorum的一个特例.

一般我们提到quorum(或majority)时, 都是指一个节点集合Q, 本文中我们把一个系统中所有quorum的集合记为: \(\mathbb{Q} = \{ Q_1, Q_2... \}\), 其中 \(Q_k = \{a_i, a_j...\}\) 是一个节点(paxos中的Acceptor)的集合, 例如一个三节点系统{a, b, c}, 它的majority的quorum集合:

\[\begin{bmatrix} \mathbb{Q} = \{ & \{a, b\}, \\ & \{b, c\}, \\ & \{c, a\}, \\ & \{a, b, c\} \\ \} \\ \end{bmatrix}\]

现在再回到问题, 要保证quorum-rw的正确性, 就要求一次成功的写入, 必须能成功读取, 从这点看, 过半数这个要求是可以放宽的:

只需要quorum保证任意2个quorum有交集就可以.

在paxos made simple中, 也就是classic paxos的paper中, Leslie Lamport 还在使用majority这个名称来表示多数派, 在后面的paper, fast-paxos, generalized paxos中,都换成了quorum这个名词.

虽然在paper中都是”majority”的意思, 但quorum的适用范围更广.

我们看几个非majority的quorum的例子, 这些quorum都不是传统意义上的majority, 但都可以实现majority同样的功能, 为quorum-rw或paxos提供正确性保证:

不是majority的quorum们

带权重的quorum

{a, b, c, d, e} 5个节点中, 把a, b, c三个节点部署到一起: { abc, d, e}(abc必须同时选). 如果选abc, 就记3票, d, e只记一票.

3个成员一共5票, 所有票数过半的集合都是quorum: {abc}, {abc, d}, {abc, e}, {abc, d, e}. 但{d, e} 不是一个quorum, 因为根据我们的定义, 只有2票没有过半.

这样, 任意2个quorum都有交集{abc}. 那么quorum-rw算法, 如果选择任意一个quorum写, 另一个进程选择任意一个quorum读, 都可以实现安全的读写.

包含特定元素的quorum

从上面的例子, 可以直接去掉majority的概念, 就是一类特殊的quorum集合: \(\mathbb{Q}\) 中每个quorum都必须包含某个特定元素:

如果集群是3个节点{a,b,c}, 定义每个quorum都必须包含a, 那么: \(\mathbb{Q} = \{ \{a\}, \{a,b\}, \{a,c\}, \{a,b,c\} \}\).

任意2个quorum都有交集{a}, 用这个quorum定义来运行paxos, 仍然是正确的. (可以试试跑一个之前 paxos的直观解释 中的例子里的paxos)

4/5 加 2/5的quorum

在一个5节点集群{a,b,c,d,e} 中, quorum定义为:至少包含4个元素, 或是{a,b} 那么\(\mathbb{Q}\) 就是:

{a, b, c, d}
{a, b, c, e}
{a, b, d, e}
{a, c, d, e}
{b, c, d, e}
{a, b}

任一4个元素的quorum都有交集, 任一4元素的quorum也和{a,b}有交集. 能用来跑paxos.

Hierarchical quorum 3x3

hierarchical quorum 是一个分层的quorum定义, 假设集群有9个节点, 排列成3x3的矩阵, 这里quorum的定义为: 至少包括2行, 每行中至少包含2个节点.

容易看出任意2个quorum必有交集, 例如 {a1, a2, b1, b2} 和 {b2, b3, c2, c3} 有一个交集{b2}:

.------.
|a1  a2| a3
|   .--|---.
|b1 |b2| b3|
'------'   |
c1  |c2  c3|
    '------'

以此quorum定义替代majority, 运行多数派读写或paxos一样是正确的.

Hierarchical quorum 2xn

继续沿用hierarchical quorum 的定义, 但只选2行. 因为一个2节点的系统{x, y}, quorum集合可以是 \(\mathbb{Q} = \{ \{x\}, \{x, y\} \}\) (或 \(\mathbb{Q} = \{ \{x, y\}, \{y\} \}\) ), (这里x, y代表一行).

于是这个场景中的quorum 可以描述为: 包含第一行的majority, 或在每一行都包含一个majority:

a1 a2 a3
b1 b2 b3 b4 b5

容易看出按照这个规则选出的quorum, 任意2个都有交集. 例如:

{a1, a3}
{
  a1, a2,
  b1, b2, b3,
}

有交集{a1}.

raft 使用了这种quorum定义来完成集群变更, 基于hierarchical quorum的选主在raft中叫做joint consensus.

通过设计 quorum 降低延迟

任何一种quorum的定义, 都可以用来替代majority来实现quorum-rw, 或paxos, 并严格保证正确性. 但是, 选择一种quorum, 将直接影响系统的性能和可用性.

首先最直观的结论是, quorum定义中所需的节点个数越少, 完成一次quorum-rw或paxos的消息量就越少, 如果可以选择到更近的节点, 那么整个系统的延迟就有可能会降低.

quorum 决定了系统的可用性

另一方面, 不同的quorum的选择, 会直接影响系统的可用性:

任何一种quorum的选择, 可用性都低于majority的quorum.

非majority的quorum, 允许更少的可用节点, 以3x3的hierarchical quorum存储为例, 一次写入如果选择了左上的4个节点, 就达到了quorum要求, 只需要不到半数的节点参与. 看似容忍了更多(5个)故障, 但它整体的可用性要低于majority的quorum.

.-----.
|a1 a2| a3
|b1 b2| b3
'-----'
c1  c2  c3

系统可用性的 quorum 定义

一个分布式系统的可用性, 可以从一下几方面去考虑, 假设:

• 集群中的节点随机停机;
• 并假设一段时间内一个服务器停机时间比例p=0.01(差不多相当于一个服务器一年有3天左右的时间不在线);
• 且停机事件彼此独立.

某个时刻, 如果在线的节点集合是一个quorum, 那系统就可用, 可以通过在线节点集合这个quorum完成多数派读写或paxos; 否则就是系统不可用.

🌰 例如 {a, b, c} 三个节点, 选择majority的quorum,

• a, b 在线, c停机时, {a, b} 是一个quorum 所以系统可以正常运行.
• 如果a在线, b, c都停机, {a} 不是一个quorum, 所以系统这时就不可用了.

因此整个系统的可用性可以定义为: 每个quorum出现的概率之和: \(P( \mathbb{Q} ) = ΣP(Q_i), Q_i ∈ \mathbb{Q}\). quorum出现的概率是: P(Qᵢ) = (1-p)ˣpⁿ⁻ˣ, 其中x是一个quorum包含的节点个数: x = |Qᵢ|.

🌰 对一个三节点的系统 {a, b, c} majority 的quorum集合 \(\mathbb{M} = \{ \{a, b\}, \{b, c\}, \{c, a\}, \{a, b, c\} \}\), 那么3个节点可能出现的所有状态, 以及对应的整个系统是否可用如就如下展示:

0)  {}        (1-p)⁰p³    // unavailable
1)  {a}       (1-p)¹p²    // unavailable
2)  {b}       (1-p)¹p²    // unavailable
3)  {c}       (1-p)¹p²    // unavailable
4)  {a, b}    (1-p)²p¹    // available
5)  {b, c}    (1-p)²p¹    // available
6)  {c, a}    (1-p)²p¹    // available
7)  {a, b, c} (1-p)³p⁰    // available

如果选择majority的quorum来构建系统, 那系统可用的概率是后4行状态概率相加: C(3, 2)(1-p)²p¹ + C(3, 3)(1-p)³p⁰ ~= 1-4p² ~= 0.9996, 大约3个9

如果选择另一种quorum, 例如去掉{a, b}, 加入{c}, 那这时可用性是第3, 5, 6, 7行相加: (1-p)¹p² + 2 (1-p)²p¹ + (1-p)³p⁰ = 1-p, 大约2个9, 此时系统中每个quorum都包含c, c在线或停机直接决定了系统的可用性, 所以系统可用性也就是直接等于了c节点的可用性.

quorum 的可用性分析

然后我们来看看为什么非majority的quorum 会降低系统的可用性:

• 假设majority quorum的集合为 \(\mathbb{M}\), 也就是所有大小过半的节点集合;
• 对某一个quorum集合\(\mathbb{Q} = \{Q_1, Q_2...\}\), 其中 \(Q_k = \{a_i, a_j...\}\) 是一个节点集合, Qₓ满足对quorum的定义: 任意2个Qᵢ, Qⱼ交集都不为空: \(Q_i ∩ Q_j ≠ \emptyset\);
• 单机停机几率 p = 0.01;

我们可以对\(\mathbb{Q}\) 做一个变换 \(f(\mathbb{Q})\):

从 \(\mathbb{Q}\) 中选择最小的一个Qᵢ: Qᵢ满足∀Qⱼ: |Qᵢ| ≤ |Qⱼ| (如果有多个最小的, 选任意一个), 从\(\mathbb{Q}\) 中去掉Qᵢ, 再把Qᵢ的补集加入:

\[\mathbb{Q}' = {\mathbb{Q}} \backslash \{ Q_i\} ∪ \{\overline{Q_i}\}\]

\(\mathbb{Q}'\)也还是一个合法quorum集合: 因为对任意一个Qⱼ, 如果\(|Q_j| ≥ |Q_i|\) 且 \(Q_j ≠ Q_i\), 那么Qⱼ一定包含一个不在Qᵢ中的节点, 所以 \(\overline{Q_i}\) 和 \(Q_j\) 一定有交集.

重复这个步骤直到 \(\mathbb{Q}\) 中所有quorum的大小都大于半数. 最后 \(\mathbb{Q}\) 就变成了一个\(\mathbb{M}\) 的子集: \(f(\mathbb{Q}) ⊆ \mathbb{M}\)

这样, 任何一个 \(\mathbb{Q}\) 都可以跟 \(\mathbb{M}\) 的一个子集建立一个一一映射. 而 \(\mathbb{M}\) 的子集的可用性一定不大于 \(\mathbb{M}\) 的可用性: \(P(subset(\mathbb{M})) ≤ P(\mathbb{M})\).

而且, 对一个不大于半数的Qᵢ(x = |Qᵢ| ≤ ⌊n⌋/2), 它的补集在随机停机过程中出现的几率更大:

\[(1-p)^xp^{n-x} ≤ (1-p)^{n-x}p^x ⇒ P(Q_i) ≤ P(\overline{Q_i}) ⇒ P(\mathbb{Q}) ≤ P(f(Q))\]

∴ \(P(\mathbb{Q}) ≤ P(f(\mathbb{Q})) ≤ P(\mathbb{M})\), 即 majority 的 quorum 可靠性最高. 其他任何一种quorum的选择, 即使它允许更多的节点停机, 也只能提供较低的可用性.

🌰 例如我们算下, 3x3 的 hierarchical quoru m的可用性:

• majority 3 节点的停机概率是: Pm3 = C(3, 2)(1-p)²p + C(3, 3)(1-p)³
• Pm3也就是每个机房的停机概率, 把每个机房看做一个大的节点, 因此3个机房组成的majority quorum的不在线几率是: Ph9 = C(3, 2)(1-Pm3)²Pm3 + C(3, 3)(1-Pm3)³

我们用 hierarchical-quorum.py 这个小程序计算如下:

failure-rate:
  majority of 3 nodes:        2.98e-04
  majority of 7 nodes:        3.42e-07
  majority of 9 nodes:        1.22e-08
  hierarchical quorum of 3x3: 2.66e-07

可以看到hierarchical 3x3 的可用性比majority 9节点的可用性要低1个9. 差不多相当于7节点的majority 可用性.

应用场景

zookeeper 使用 hierarchical quorum 的例子

🌰 zookeeper 的配置允许分组的概念, 就是使用了这种quorum定义, 它允许多于半数(5个/9个)节点停机. 例如在我们之前实现的3机房部署中, 就使用了3个机房(DC), 每个机房3个zookeeper实例的配置:

            zookeeper
                |
    .-----------+----------.
   /            |           \
  DC-1         DC-2         DC-3
 / | \        / | \        / | \
a1 a2 a3     b1 b2 b3     c1 c2 c3
--------     --------     --------
   | `- 30ms -'    `- 30ms -' |
   `---------- 60ms ----------'

hierarchical quorum 的一个优势在于在系统可用的状态下, 只需要联系2个机房就可以完成一次读写.

我们假设一个接近现实场景:

• DC-1 和 DC-2之间的延迟是30ms,
• DC-2 和 DC-3之间也是30ms,
• DC-1 和 DC-3之间比较远, 延迟是60ms,

那么选择 hierarchical quorum 所产生的延迟就在一定概率上比majority quorum的延迟低.

例如, 现在只观察DC-1的写入请求, 最优情况下它只需联系最近的机房(DC-2)来完成一次paxos. 如果宕机2个节点:

• hierarchical quorum 需要联系DC-3的条件是: 这2个宕机节点都集中在DC-1或都集中在DC-2时;
• majority quorum 需要联系DC-3的条件是: 这2个宕机节点都不在DC-3时.

在宕机2个节点时, hierarchical 只有 majority 40% 的几率延迟达到 60ms; 如果假设单个节点停机几率是p=0.01(1年有3, 4天不在线), 那么9节点宕机2个节点的几率大约是0.0033, 差不多在99分位上, 延迟可以从60ms降低到30ms.

用 quorum 来优化链路选择: 边缘存储场景

🌰 传统的存储+CDN架构是用户传输到中心, 之后在下载时, 再通过边缘机房访问, 边缘机房没有则回中心拉取. 且边缘机房之间没有架构级别的关联, 各自在设计上是独立的:

Center Storage + CDN:
            client
            |  ↑
            |  |
  edge DCs  |  e₁   e₂   e₃
            |    ↖  ↑  ↗
center DC   `-----→ c

假设我们现在有一个边缘存储的系统: 3个分布在各地的边缘机房eᵢ, 和一个中心机房c.

Edge Storage:
               client
               ↑
               ↓
  edge DCs     e₁ - e₂ - e₃   // weight = 1
                 \  |  /
center DC           c         // weight = 2

• 边缘存储的特点是, 一个中心机房c, 一般包含全量数据, 做数据的集中处理, 归档等. 写入一般分散在各个边缘机房, 方便就近接入用户请求. 可以把边缘存储想象成支持本地就近上传的CDN.

• 边缘跟中心的链路一般很好. 但也会有故障, 边缘跟边缘之间链路质量一般. 因此在处理用户写请求时, 尽可能让边缘机房eᵢ优先选择跟中心机房c同步, 当联系不到中心机房时, fallback到几个边缘机房之间达成一致完成一笔写入.

  边缘存储的架构相比传统存储+CDN的模式, 可以让写入直接落在边缘机房, 省去了一次不必要的带宽.

在这个例子中, 我们设置中心机房c权重为2; 3个边缘机房, 权重各为1, quorum定义成带权重的quorum: 一个quorum所包含的节点权重之和至少为3.

假设有1笔写入出现在e₁, 如果它跟中心机房c可以直接通信, 那就通过quorum {e₁, c} 直接完成一次多数派写入. 或者当时跟中心连接抖动, 那么它也可以联系e₂, e₃, 通过quorum {e₁, e₂, e₃}完成一次多数派写入.

总结: quorum 在分布式系统中的意义

几年前在一个机房里用paxos协同起来的分布式系统, 可以看做是分布式的从0到1的一步, 解决了分布问题.

分布式系统近年的发展越来越倾向于异构, 非对等, 大规模的架构共存于一个系统内. 这就对一致性算法提出了新的要求, 现代分布式系统都在尝试解决从1到100的问题: 将可用的系统打造成适应各种复杂场景的可靠系统(而不是简单的单机房几个服务器的单一场景): 系统在节点延迟/故障率/性能等变得越来越复杂的情况下, 系统设计的重心从正确性转移到调优方面, 例如如何让读写倾向于集中在高性能或更稳定的节点上, 或者让读写的流量优先最近的.

通过选择合适的quorum, 我们可以在这些复杂一些的系统中, 允许业务在可用性, 延迟, 性能之间做一个权衡:

• 减少消息数量/延迟, 例如像zookeeper hierarchical quorum中的异地多活的例子, 可用性从8个9降低到7个9(假设7个9够用了:D), 换来更稳定的写入延迟: P99 延迟可以从60ms降低到30ms.

• 使用加权重的quorum, 来实现边缘存储这种非对等系统中的链路选择和fallback机制.

• 或实现更灵活的配置变化, 例如raft 的成员变更算法.

本文链接: https://blog.openacid.com/algo/quorum/

• [raft]: https://raft.github.io/
• [joint consensus]: https://github.com/peterbourgon/raft/blob/master/JOINT-CONSENSUS.md
• [Classic Paxos]: http://lamport.azurewebsites.net/pubs/pubs.html#paxos-simple
• [Fast Paxos]: http://lamport.azurewebsites.net/pubs/pubs.html#fast-paxos
• [paxos的直观解释]: https://blog.openacid.com/algo/paxos
• [Leslie Lamport]: http://www.lamport.org/
• [多数派读写]: https://zh.wikipedia.org/wiki/Quorum_(分布式系统)
• [paxos made simple]: http://lamport.azurewebsites.net/pubs/pubs.html#paxos-simple
• [hierarchical quorum]: https://zookeeper.apache.org/doc/r3.3.2/zookeeperHierarchicalQuorums.html
• [hierarchical-quorum.py]: /post-res/quorum/hierarchical-quorum.py
• [zookeeper]: https://zookeeper.apache.org/
• [slide-10]: https://blog.openacid.com/algo/paxos/#slide-10
• [slide-20]: https://blog.openacid.com/algo/paxos/#slide-20