Erasure-Code-擦除码-3-极限篇

本文链接: https://blog.openacid.com/storage/ec-3/

书接上回

上一篇 第二篇:实现 中, 我们介绍完了基于GF(2⁸)伽罗瓦域的标准实现以及做了正确性分析, 我们也提到:

在EC的计算中, 编解码是一个比较耗时的过程, 因此业界也在不断寻找优化的方法, 不论从理论算法上还是从计算机指令的优化上, 于是下一篇我们将介绍如何把EC实现为一个高效的实现.

本文我们来介绍, 在实际生产环境使用时还需做哪些优化, 来将EC打造成一个高效的实现.

• 第一篇:原理 再上一篇 🤔
• 第二篇:实现 上一篇 🤔
• 第三篇:极限 我们在这 😁

优化从两方面入手, 一方面是如何加快运算, 一方面是如何减少运算.

运算优化

我们先根据一些基本的假设来计算下EC的计算开销有多少, 首先是EC编码过程是:

编码解码开销

假设EC配置是k+m, k个数据库编码成m个校验块. EC的编码就是矩阵相乘:

\[\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_m \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & 2 & 2^2 & \dots & 2^{k-1} \\ 1 & 3 & 3^2 & \dots & 3^{k-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & m & m^2 & \dots & m^{k-1} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_k \end{bmatrix}\]

生成每一个校验块的计算工作是 yᵢ = Σ aᵢⱼ ⊗ dⱼ

⊗ 表示GF(2⁸) 下的乘法, Σ表示GF(2⁸)下的求和, 也就是XOR, 每个校验块的生成就需要k个GF(2⁸)的乘法, 以及k-1次(计算时假设为k次)XOR操作. 而之前我们提到的GF(2⁸)中的乘法和除法是通过查指数表计算的 :

\[\begin{aligned} a * b = 2^{log_2a+log_2b} \end{aligned}\]

也就是说一次GF(2⁸)的一次乘法运算需要: 2次查对数表求得 log₂a和log₂b, 一次加法, 最后再查一次指数表, 再算上最后的求和运算, 生成一个校验块的操作需要 3 * k 个查表, 2 * k 个计算. 查表看做L1 cache的访问, 大约1纳秒. XOR计算指令大约0.5 纳秒.

编码 1 byte 开销大约是4 * k 纳秒.

GF(2⁸)下的指数表和对数表都是256字节, 假设cpu的L1 cache line有足够空间, 查表都在L1 cache中完成.

Intel Core i7-9xx CPU的L1 data cache有32KB.

L1 Cache 访问延迟 为 4个cycle, 约1~2纳秒.

数据解码开销分为2部分, 一个是矩阵求逆, 一个是逆矩阵跟没有丢失数据的乘法计算. 其中主要是第2部分, 它跟编码过程一样也是计算一个矩阵乘法: uᵢ = Σ aᵢⱼ ⊗ xⱼ, 也需要4 * k 纳秒.

矩阵求逆的操作开销可以忽略, 因为一般情况下, 丢失的数据都是一整块(例如12+4的EC组中, 每个数据块都是64MB大小的) 对一组EC编码的数据, 只需要求一次逆就可以了.所以均摊开销很小.

在k+m = 12+4 的EC配置下, 一个CPU上的编/解码速度大约是1秒/(4*12)纳秒 = 19MB/秒 .

机械盘的顺序读写差不多是100MB/s, 25Gbps的网线快普及了, 每秒读写3GB数据, SSD就不说了, 一个EC数据修复速度才19MB/s? 不行不行.优化!

直接的优化方式包括2方面:

• 减少查表次数,
• 以及通过并行指令使得多个查表或计算的工作在一个指令内完成.

优化查表次数

为了优化查表次数, 我们可以将基于指数表和对数表的乘法实现: a * b = 2^(log₂a + log₂b) 优化成直接查询一个乘法表, 但这个表太大, 有256x256个字节=64K, 可能超出L1 cache的大小, 导致查表效率直线下降(一般L1 cache和L2 cache的查询效率相差几倍)

于是为了减少查表次数, 我们首先必须减小表的大小.

构造小乘法表

因为一个 8-bit 的数字 a=hhhhllll 可以表示成 2 个 4-bit 的数字(hhhh0000 ^ llll):

a = a₇ a₆ a₅ a₄ a₃ a₂ a₁ a₀
  = a₇ a₆ a₅ a₄ 0  0  0  0  ^  a₃ a₂ a₁ a₀
  = h ⊗ 2⁴ ^ l

于是我们可以把2个 8-bit 数的乘法拆成2个 4-bit数 乘 8-bit数 之和:

y ⊗ a = (y ⊗ 2⁴ ⊗ h) ^ (y ⊗ l).

这样所需的乘法表就很小了, 只有16x256 = 4KB大小(y和y⊗2⁴的取值有256个, h/l的取值有16个), 完全可以放入L1 cache中. 而对应的GF(2⁸)下的乘除法计算也需要做一些调整, 但首先我们需要证明一下这种拆分的正确性:

移位和乘法在GF(2⁸)的等价

根据在上一篇的 质多项式 的解释, 在GF(2⁸) 下, h ⊗ 2⁴ 和 h<<4 是等价的, 因为根据GF(2⁸)下的乘法定义是 a ⊗ b % P₈(P₈ = x⁸ + x⁴ + x³ + x² + 1);

h只有4个bit, 它对应的多项式最高次数项是x³, 2⁴对应的多项式是x⁴, 所以它们2个相乘最高次幂是x⁷, 不会超过P₈, 所以取模结果跟移位结果一样.

而h ⊗ 2⁵ 跟 h<<5 在GF(2⁸)下不是等价, h<<5最高次幂是8, 取模之后值就可能发生了变化.

举个例子, 回顾下我们在 上一篇 中生成的指数表, 可以看到对所有的a=0000xxxx形式的数, a ⊗ 2⁴ 和 a<<4的结果是一样的, a ⊗ 2⁵ 跟 a<<5 就不一样了:

01 ⊗ 2⁴ == 01<<4
 .---------.
/           ↘
01 02 04 08 10 20 40 80 1d 3a 74 e8 cd 87 13 26
4c 98 2d 5a b4 75 ea c9 8f 03 06 0c 18 30 60 c0
9d 27 4e 9c 25 4a 94 35 6a d4 b5 77 ee c1 9f 23
           0a ⊗ 2⁴ == 0a<<4
          .---------.
         /           ↘
46 8c 05 0a 14 28 50 a0 5d ba 69 d2 b9 6f de a1
         \              ↗
          '------------'
           0a ⊗ 2⁵ != 0a<<5
5f be 61 c2 99 2f 5e bc 65 ca 89 0f 1e 3c 78 f0
fd e7 d3 bb 6b d6 b1 7f fe e1 df a3 5b b6 71 e2
d9 af 43 86 11 22 44 88 0d 1a 34 68 d0 bd 67 ce
81 1f 3e 7c f8 ed c7 93 3b 76 ec c5 97 33 66 cc
85 17 2e 5c b8 6d da a9 4f 9e 21 42 84 15 2a 54
a8 4d 9a 29 52 a4 55 aa 49 92 39 72 e4 d5 b7 73
e6 d1 bf 63 c6 91 3f 7e fc e5 d7 b3 7b f6 f1 ff
e3 db ab 4b 96 31 62 c4 95 37 6e dc a5 57 ae 41
82 19 32 64 c8 8d 07 0e 1c 38 70 e0 dd a7 53 a6
51 a2 59 b2 79 f2 f9 ef c3 9b 2b 56 ac 45 8a 09
12 24 48 90 3d 7a f4 f5 f7 f3 fb eb cb 8b 0b 16
2c 58 b0 7d fa e9 cf 83 1b 36 6c d8 ad 47 8e 01

根据h ⊗ 2⁴ 和 h<<4的等价, 我们就可以拆分 y ⊗ a = (y ⊗ 2⁴ ⊗ h) ^ (y ⊗ l). 然后利用16x256的乘法表来实现更快的GF(2⁸)下的乘法.

并行查表 SIMD

在上面乘法优化的基础上, 下一个计算优化是将查表并行处理, 这主要通过使用SIMD 指令来实现.

SIMD 是优化的主要手段, 同时对一组数据（又称“数据向量”）中的每一个分别执行相同的操作从而实现空间上的并行性的技术. 例如Intel的MMX或SSE，以及AMD的3D Now!指令集.

mm_shuffle_epi8(u, v) 可以一次对2 个128bit的整数操作:

• u 被当做是一个16个元素, 每个元素8bit的table, 在我们这个场景中u是 y ⊗ 所有 0000xxxx 的值或y ⊗ 所有 xxxx0000的值.
• v是16 个index, 在我们的场景中是16个不同的aᵢ的高4bit或低4bit.

假设有一组乘法需要查表计算时:

u₁ = y ⊗ a₁
u₂ = y ⊗ a₂
u₃ = y ⊗ a₃
...

首先准备好这2个表:

tableL = [y ⊗ 00, y ⊗ 01, y ⊗ 02 ... y ⊗ 0f]
tableH = [y ⊗ 00, y ⊗ 10, y ⊗ 20 ... y ⊗ f0]

然后计算过程就如下所述:

• 加载tableL 到128bit的寄存器u,
• 取16个aᵢ的低4bit: lᵢ存储到寄存器v,
• mm_shuffle_epi8(y, lᵢ)
• 加载tableH 到128bit的寄存器u,
• 取16个aᵢ的高4bit: hᵢ存储到寄存器v,
• mm_shuffle_epi8(y, hᵢ)

整个乘法操作需要2次查表4个计算, 大约4纳秒, 因为一次可以计算16个8bit整数的乘法, 平均每个乘法0.25 纳秒.

同样加法也可以功过并行指令来优化, 每个加法平均需要0.06个指令.

再回头看编解码计算 uᵢ = Σ aᵢ xᵢ

编解码平均就只需要0.31 * k 纳秒. 简单估计就比之前的4*k纳秒减少到1/10, 至少每秒可以恢复300MB的数据了.

几乎所有的EC实现都使用了并行优化, 包括 Jerasure, Intel ISA-L 这2个c实现.

如果你需要go版本的实现, 请移步我的前任(同事)xxx同学的实现, benchmark比Intel ISA-L还要快一点: reedsolomon.

关于实现设计可以参考xxx同学的博客: 实现高性能纠删码引擎.

8102年跟大家一起做EC时, 设计2个月, 编码1个月, 当时碰巧在某乎撩到了xxx同学, 有他的加入, 还有当时一起的几个棒小伙(小妹), 才能顺(mian)利(qiáng)完成. 这一版的go实现在当时内部版本中又增加了垃圾回收支持, 更新EC组数据的快速合并等.

算法优化

计算开销的优化之后我们来看看在算法层面的优化. EC的解码开销主要来自于需要对k组数据同时进行计算, 才能解码一个数据块. 如果能降低整体恢复所需的数据, 那解码开销将在计算优化的基础上进一步降低.

数据恢复IO优化: LRC

当 EC 进行数据恢复的时候, 需要k个块参与数据恢复, 直观上, 每个数据块损坏都需要k倍的IO消耗.

为了缓解这个问题, 一种略微提高冗余度, 但可以大大降低恢复IO的算法被提出: [Local-Reconstruction-Code], 简称 LRC.

LRC的思路很简单, 在原来的 EC 的基础上, 对所有的数据块分组对每组在做1次 k’ + 1 的 EC. k’ 是二次分组的每组的数据块的数量.

LRC 的校验块生成

\[\begin{aligned} \overbrace{d_1 + d_2 + d_3}^{y_{1,1}} & + \overbrace{d_4 + d_5 + d_6}^{y_{1,2}} & = y_1 \\ d_1 + 2d_2 + 2^2d_3 & + 2^3d_4 + 2^4d_5 + 2^5d_6 & = y_2 \\ d_1 + 3d_2 + 3^2d_3 & + 3^3d_4 + 3^4d_5 + 3^5d_6 & = y_3 \end{aligned}\]

最终保存的块是所有的数据块: d₁, d₂, d₃, d₄, d₅, d₆ , 和校验块 y₁₁, y₁₂, y₂, y₃.

这里不需要保存 y₁ 因为 y₁ = y₁₁ ^ y₁₂ .

对于 LRC的EC来说, 它的生成矩阵前k行不变, 去掉了标准EC的第k+1行(全1的行), 多出2个局部的校验行:

\[\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \hline \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 \\ \hline \\ 1 & 2 & 2^2 & 2^3 & 2^4 & 2^5 \\ 1 & 3 & 3^2 & 3^3 & 3^4 & 3^5 \\ \end{bmatrix} \times \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \\ d_6 \end{bmatrix} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \\ d_6 \\ y_{11} \\ y_{12} \\ y_2 \\ y_3 \\ \end{bmatrix}\]

LRC 的数据恢复

LRC 的数据恢复和标准的EC类似, 除了2点不同:

• 在选择校验块的行生成解码矩阵的时候, 如果某第k+i行没有覆盖到任何损坏的数据的话, 是无法提供有效性信息, 需要跳过的.

  例如 d₄ 损坏时, 不能像标准EC那样选择第7行 1 1 1 0 0 0 这行作为补充的校验行生成解码矩阵, 必须略过第7行, 使用第8行.

• 不是所有的情况下, m个数据损坏都可以通过加入m个校验行来恢复. 例如d₁, d₂, y₂, y₃ 损坏时就是无法恢复的, 因为y₁₂ 用不上

  例如在12数据块, 4个校验块中前2个是LRC校验块的情况下, 只有87%的损坏是能恢复的.

如果你需要一个LRC的c实现, 移步此处: lrc-erasure-code

Hitchhiker EC算法

Hitchhiker 可以认为是基于LRC的进一步优化. paper太繁琐, 核心思想挺简单:

Hitchhiker 编码过程

为了开始说明原理, 取一个有代表性的例子: 对一组数据k=6: d₁, d₂…d₆ 做3,3的LRC编码:

y₁₁ = d₁ + d₂ + d₃
y₁₂ = d₄ + d₅ + d₆

y₁ = y₁₁ + y₁₂

y₂ = d₁ + 2d₂ + 2²d₃ + 2³d₄ + 2⁴d₅ + 2⁵d₆
y₃ = d₁ + 3d₂ + 3²d₃ + 3³d₄ + 3⁴d₅ + 3⁵d₆

对另一组数据k=6: e₁, e₂…e₆ 做标准EC的编码:

z₁ = e₁ + e₂ + e₃ + e₄ + e₅ + e₆
z₂ = e₁ + 2e₂ + 2²e₃ + 2³e₄ + 2⁴e₅ + 2⁵e₆
z₃ = e₁ + 3e₂ + 3²e₃ + 3³e₄ + 3⁴e₅ + 3⁵e₆

存储的时候, 将d/e对应的编号的数据块作为一个数据块存储到一起, 同时对应的校验块做如下规则的存储:

• 校验块1 是 (y₁, z₁)
• 校验块2 是 (y₂, z₂+y₁₁)
• 校验块3 是 (y₃, z₃+y₁₂)

也就是说, 把第一组的LRC校验块, 跟第2组的某些校验块XOR之后一起存储:

d₁  d₂  d₃  d₄  d₅  d₆ | y₁ y₂     y₃
e₁  e₂  e₃  e₄  e₅  e₆ | z₁ z₂+y₁₁ z₃+y₁₂

Hitchhiker 数据恢复过程

如果只有一个数据块损坏, 例如(d₁ e₁)损坏,

• 先恢复第2行, 通过 e₂ .. e₆ 和 z₁ 恢复出e₁;
• 再通过 e₁ .. e₆ 计算出z₂;
• 通过没有损坏的z₂+y₁₁和z₂的值, 计算出y₁₁;
• 通过d₂, d₃, y₁₁恢复d₁.

这样在一个EC组中, 一半数据需要k倍IO来恢复, 剩下的一半只需要k/2倍的IO来恢复. 总体来说大约节省了25%的IO开销.

而第1, 2, 3步在计算时可以合并, 只会增加有限的额外的IO.

理论上这种方法可以最多节省50%的恢复IO, 实际使用时, 因为k不能无限大, 可以节省30%的IO.

同样 Hitchhiker EC 有一份来自我前任(同事)xxx同学的go实现: xrs.

EC的可靠性分析

在可靠性方面, 假设 EC 的配置是k个数据块, m个校验块. 根据 EC 的定义,k+m个块中, 任意丢失m个都可以将其找回. 这个 EC 组的丢失数据的风险就是丢失m+1个块或更多的风险:

\[\sum_{i=m+1}^{k+m} {k+m \choose i} p^{i} (1-p)^{k+m-i}\]

这里p是单块数据丢失的风险,一般选择磁盘的日损坏率: 大约是0.0001. p一般很小所以近似数据丢失风险就只看第1项:

\[{k+m \choose m+1} p^{m+1} (1-p)^{k-1}\]

硬盘的年损坏率经验值大约是7%: 一年过去, 7%的硬盘坏掉. 那么均摊到日损坏率: (1-p)³⁶⁵ = 1 - 0.07, 可以得到p = 0.00017

在计算多副本可靠性的时候, 这里也假设一个损坏的磁盘修复的周期是1天, 也就是说1天之内同时损坏达到一定数量才会造成数据丢失. 一天之后, 数据有恢复到原来的副本数量. 所以即使冗余度不增加, 修复越快, 也可以很大程度上提高可靠性.

在这个模型下, 我们可以看下2个校验块时的几个典型的可靠性比较, 第一行k=1时, 就是1+m的EC, 实际上等同多副本的策略了.

k	m	丢数据风险
1	2	1 x 10⁻¹² (1个数据块+2个校验块 可靠性 和 3副本等价)
2	2	3 x 10⁻¹²
3	2	9 x 10⁻¹²
10	2	2 x 10⁻¹⁰ (10+2 和 12盘服务器的 RAID-6 等价)
32	2	5 x 10⁻⁹
64	2	4 x 10⁻⁸

k+m EC 的数据丢失风险:

durability	m=2	m=3	m=4
k=1	1 x 10⁻¹²	1 x 10⁻¹⁶	1 x 10⁻²⁰
k=2	3 x 10⁻¹²	5 x 10⁻¹⁶	6 x 10⁻²⁰
k=3	9 x 10⁻¹²	2 x 10⁻¹⁵	2 x 10⁻¹⁹
k=10	2 x 10⁻¹⁰	7 x 10⁻¹⁴	2 x 10⁻¹⁷
k=32	5 x 10⁻⁹	5 x 10⁻¹²	4 x 10⁻¹⁵
k=64	4 x 10⁻⁸	7 x 10⁻¹¹	1 x 10⁻¹³

但是看图更清楚:

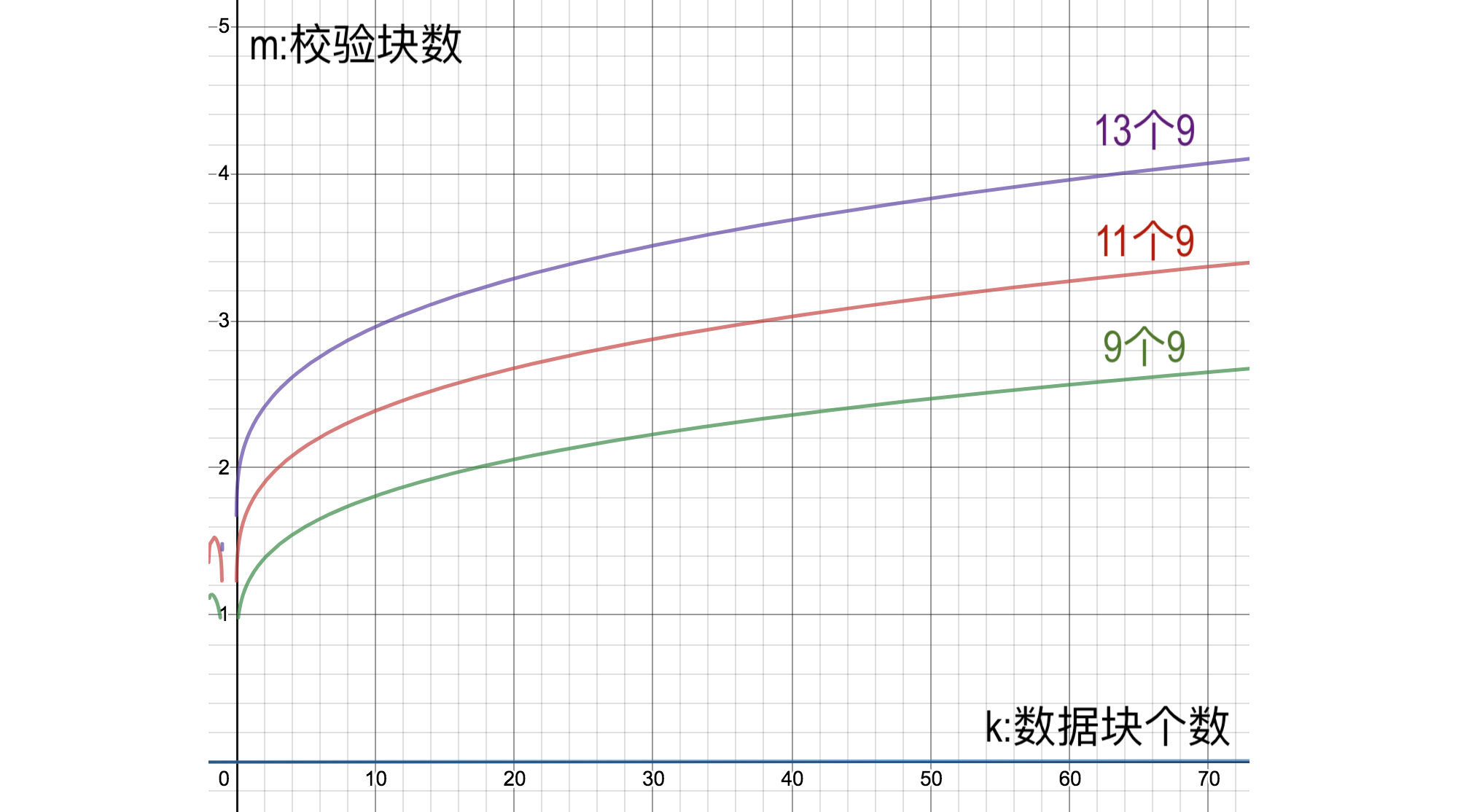
划重点!!!:

取k=1, m=2时, 相当于3副本, 大约可以达到11~12个9. 这也是aws-s3承诺的11个9的由来: s3-durability :

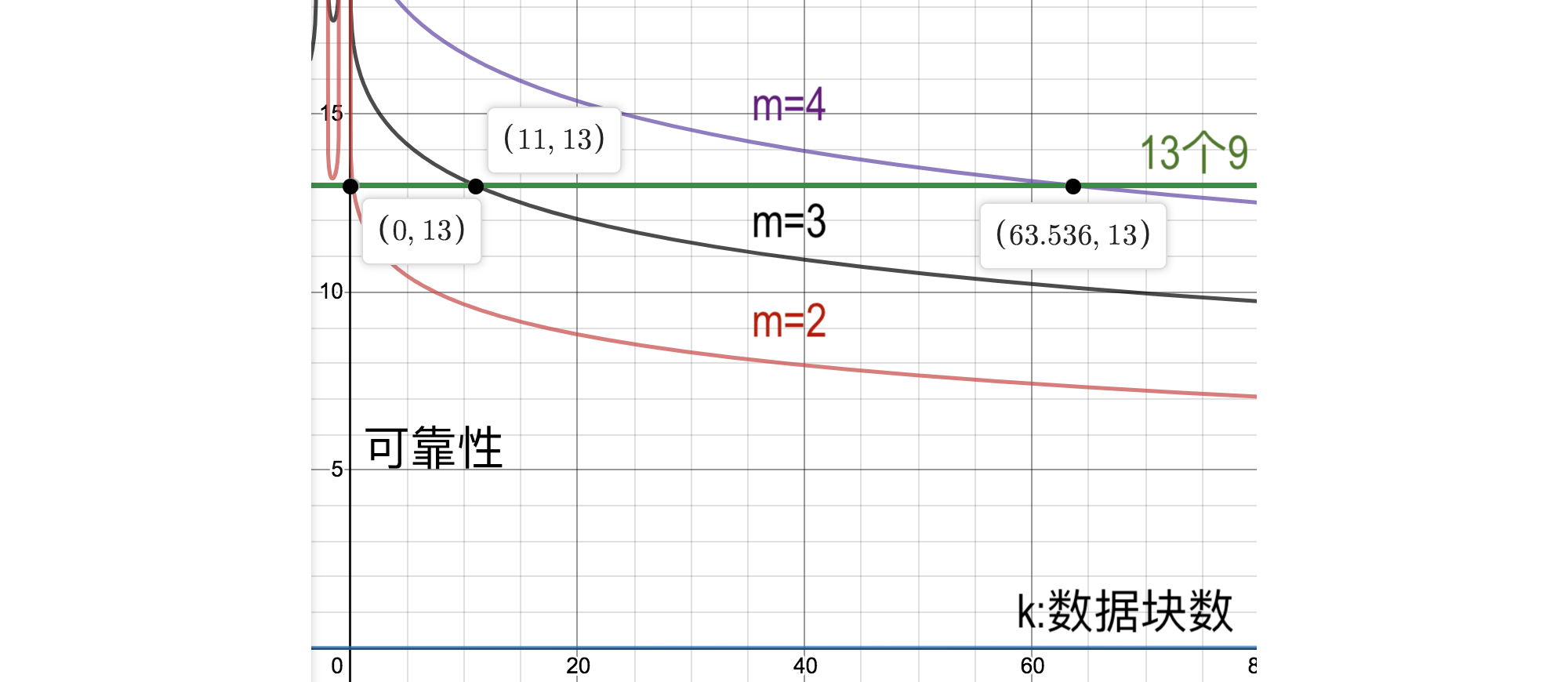
• 要达到13个9的可靠性, 2个校验块最多允许0.22个数据块.也就是说3副本无论如何也达不到13个9的可靠性.
• 要达到13个9的可靠性, 3个校验块最多允许11个数据块.
• 要达到13个9的可靠性, 4个校验块最多允许63个数据块.

同样, 如果有k个数据块要达到若干个9的可靠性, 要求的m如下:

数据修复IO消耗分析

以一个 EC 组来分析, 1个数据块一天内损坏的概率是 p=0.0001(上面算的), 这个组中有块损坏的概率是: 1 - (1-p)ᵏ⁺ᵐ 而 布鲁克·泰勒 觉得p很小所以可以近似为: (k+m)p

在标准EC的k+m实现里, 每次数据损坏都需要读取k个的数据进行恢复. 不论1块损坏还是多块损坏. 可以认为EC的修复是读取k个数据块输出m个修复的块.

于是在一天的时间内, 这个EC组修复产生的数据量是 (k+m)p * (k+m) * ECblockSize. 除以EC组总大小(k+m)*ECblockSize, 就是存储集群单位容量每天产生的修复传输量, 刚好是(k+m)p.

划重点!!!:

如果存储集群有100PB, 每天用于恢复数据产生的数据传输量: (k+m)p *总容量 =~ 0.0016 * 总容量 = 160TB;

假设单台存储服务器的容量是120TB, 整个集群有差不多1000台服务器. 每台服务器均摊的传输量是160GB/天;

而用于修复的带宽为 160GB/86400秒 = 15Mbps.

但一般来说数据恢复不会在时间上很均匀的分布, 这个带宽消耗需要预估10倍到100倍.

LRC IO开销

在一个EC组中, 损坏一个数据块的几率要远大于损坏多个数据块的几率. 如果能够及时发现坏块, 那么多数情况下只需要恢复一块就够了. 例如损坏一块的概率相比同时损坏2块的概率比例大概是:

\[\frac{ {k+m \choose 1} p (1-p)^{k+m-1} } { {k+m \choose 2} p^{2} (1-p)^{k+m-2} } = \frac{2(1-p)}{(k+m-1)p} \approx 1000\]

因此, 如果能比较快的发现坏盘, LRC的修复开销可以降低到几分之一. 同样Hitchhiker也是一样.

修复带宽是个需要关注的环节, 如果短时间内触发大量数据修复而又没有限流控制, 第一个会把磁盘IO吃光: 一个数据块需要k倍的读取来修复. 第二会把内网带宽吃光, 所有数据块/校验块都是跨机器部署的, 一个数据块的修复带来的是k个服务器的出向带宽, 如果EC存储时跨交换机, 例如每组EC的块非常随机的分布在整个集群的每台服务器上, 那么几乎所有的修复带宽都要跑遍所有的交换机.

所以EC数据块的排列在相对比较小的范围内, 也许可以避免整个局域网内的带宽耗尽.

别问我怎么知道的, 我只是猜测, 我没有经历过内网带宽被数据修复吃光并且导致大量其他业务疯狂丢包无法访问的情况.

EC系列完. 感谢大家听我叨逼叨.

EC擦除码系列:

• 第一篇:原理
• 第二篇:实现
• 第三篇:极限

本文链接: https://blog.openacid.com/storage/ec-3/

• [Vandermonde]: https://en.wikipedia.org/wiki/Vandermonde_matrix
• [Cauchy]: https://en.wikipedia.org/wiki/Cauchy_matrix
• [failure-rate]: https://www.backblaze.com/blog/hard-drive-reliability-stats-q1-2016/
• [RAID]: https://zh.wikipedia.org/wiki/RAID
• [RAID-5]: https://zh.wikipedia.org/wiki/RAID#RAID_5
• [RAID-6]: https://zh.wikipedia.org/wiki/RAID#RAID_6
• [Finite-Field]: https://en.wikipedia.org/wiki/Finite_field
• [Galois-Field]: https://en.wikipedia.org/wiki/Finite_field
• [Reed-Solomon]: https://en.wikipedia.org/wiki/Reed%E2%80%93Solomon_error_correction
• [Erasure-Code]: https://en.wikipedia.org/wiki/Erasure_code
• [Prime-Polynomial]: https://en.wikipedia.org/wiki/Irreducible_polynomial
• [Field-Extension]: https://en.wikipedia.org/wiki/Field_extension
• [Complex-Number]: https://en.wikipedia.org/wiki/Irreducible_polynomial#Field_extension
• [Hamming-7-4]: https://en.wikipedia.org/wiki/Hamming(7,4)
• [Generator-Matrix]: https://en.wikipedia.org/wiki/Generator_matrix
• [第一篇:原理]: https://blog.openacid.com/storage/ec-1
• [第二篇:实现]: https://blog.openacid.com/storage/ec-2
• [第三篇:极限]: https://blog.openacid.com/storage/ec-3
• [费马小定理的群论的证明]: https://en.wikipedia.org/wiki/Proofs_of_Fermat%27s_little_theorem#Proofs_using_group_theory
• [布鲁克·泰勒]: https://en.wikipedia.org/wiki/Taylor_series#Binomial_series
• [SIMD]: https://en.wikipedia.org/wiki/SIMD
• [质多项式]: https://blog.openacid.com/storage/ec-2/#gf2-扩张成-gf2
• [指数表]: https://blog.openacid.com/storage/ec-2/#标准ec的实现
• [Hitchhiker]: https://blog.acolyer.org/2014/12/17/a-hitchhikers-guide-to-fast-and-efficient-data-reconstruction-in-erasure-coded-data-centers/
• [s3-durability]: https://aws.amazon.com/s3/faqs/#Durability_.26_Data_Protection
• [lrc-erasure-code]: https://github.com/drmingdrmer/lrc-erasure-code
• [实现高性能纠删码引擎]: http://www.templex.xyz/blog/101/writers.html
• [reedsolomon]: https://github.com/templexxx/reedsolomon
• [xrs]: https://github.com/templexxx/xrs
• [xxx]: https://github.com/templexxx